47. Job Search VI: On-the-Job Search#
In addition to what’s in Anaconda, this lecture will need the following library:
!pip install jax
47.1. Overview#
In this section, we solve a simple on-the-job search model
based on [Ljungqvist and Sargent, 2018], exercise 6.18, and [Jovanovic, 1979]
Let’s start with some imports:
import matplotlib.pyplot as plt
import jax
import jax.numpy as jnp
import jax.random as jr
import scipy.stats as stats
from typing import NamedTuple
# Set JAX to use CPU
jax.config.update('jax_platform_name', 'cpu')
Matplotlib is building the font cache; this may take a moment.
47.1.1. Model features#
job-specific human capital accumulation combined with on-the-job search
infinite-horizon dynamic programming with one state variable and two controls
47.2. Model#
Let \(x_t\) denote the time-\(t\) job-specific human capital of a worker employed at a given firm and let \(w_t\) denote current wages.
Let \(w_t = x_t(1 - s_t - \phi_t)\), where
\(\phi_t\) is investment in job-specific human capital for the current role and
\(s_t\) is search effort, devoted to obtaining new offers from other firms.
For as long as the worker remains in the current job, evolution of \(\{x_t\}\) is given by \(x_{t+1} = g(x_t, \phi_t)\).
When search effort at \(t\) is \(s_t\), the worker receives a new job offer with probability \(\pi(s_t) \in [0, 1]\).
The value of the offer, measured in job-specific human capital, is \(u_{t+1}\), where \(\{u_t\}\) is IID with common distribution \(f\).
The worker can reject the current offer and continue with existing job.
Hence \(x_{t+1} = u_{t+1}\) if he/she accepts and \(x_{t+1} = g(x_t, \phi_t)\) otherwise.
Let \(b_{t+1} \in \{0,1\}\) be a binary random variable, where \(b_{t+1} = 1\) indicates that the worker receives an offer at the end of time \(t\).
We can write
Agent’s objective: maximize expected discounted sum of wages via controls \(\{s_t\}\) and \(\{\phi_t\}\).
Taking the expectation of \(v(x_{t+1})\) and using (47.1), the Bellman equation for this problem can be written as
Here nonnegativity of \(s\) and \(\phi\) is understood, while \(a \vee b := \max\{a, b\}\).
47.2.1. Parameterization#
In the implementation below, we will focus on the parameterization
with default parameter values
\(A = 1.4\)
\(\alpha = 0.6\)
\(\beta = 0.96\)
The \(\text{Beta}(2,2)\) distribution is supported on \((0,1)\) - it has a unimodal, symmetric density peaked at 0.5.
47.2.2. Back-of-the-envelope calculations#
Before we solve the model, let’s make some quick calculations that provide intuition on what the solution should look like.
To begin, observe that the worker has two instruments to build capital and hence wages:
invest in capital specific to the current job via \(\phi\)
search for a new job with better job-specific capital match via \(s\)
Since wages are \(x (1 - s - \phi)\), marginal cost of investment via either \(\phi\) or \(s\) is identical.
Our risk-neutral worker should focus on whatever instrument has the highest expected return.
The relative expected return will depend on \(x\).
For example, suppose first that \(x = 0.05\)
If \(s=1\) and \(\phi = 0\), then since \(g(x,\phi) = 0\), taking expectations of (47.1) gives expected next period capital equal to \(\pi(s) \mathbb{E} u = \mathbb{E} u = 0.5\).
If \(s=0\) and \(\phi=1\), then next period capital is \(g(x, \phi) = g(0.05, 1) \approx 0.23\).
Both rates of return are good, but the return from search is better.
Next, suppose that \(x = 0.4\)
If \(s=1\) and \(\phi = 0\), then expected next period capital is again \(0.5\)
If \(s=0\) and \(\phi = 1\), then \(g(x, \phi) = g(0.4, 1) \approx 0.8\)
Return from investment via \(\phi\) dominates expected return from search.
Combining these observations gives us two informal predictions:
At any given state \(x\), the two controls \(\phi\) and \(s\) will function primarily as substitutes — worker will focus on whichever instrument has the higher expected return.
For sufficiently small \(x\), search will be preferable to investment in job-specific human capital. For larger \(x\), the reverse will be true.
Now let’s turn to implementation, and see if we can match our predictions.
47.3. Implementation#
We will set up a NamedTuple that holds the parameters of the model described above
class JVWorker(NamedTuple):
A: float
α: float
β: float # Discount factor
a: float # Parameter of f
b: float # Parameter of f
grid_size: int
mc_size: int
ɛ: float
x_grid: jnp.ndarray
f_rvs: jnp.ndarray
def create_jv_worker(A=1.4, α=0.6, β=0.96, a=2, b=2,
grid_size=50, mc_size=100, ɛ=1e-4,
key=jr.PRNGKey(0)):
"""
Create a JVWorker instance with computed grids and random draws.
"""
# Generate random draws for Monte Carlo integration
f_rvs = jr.beta(key, a, b, (mc_size,))
# Max of grid is the max of a large quantile value for f and the
# fixed point y = g(y, 1)
grid_max = max(A**(1 / (1 - α)), stats.beta.ppf(1 - ɛ, a, b))
# Human capital grid
x_grid = jnp.linspace(ɛ, grid_max, grid_size)
return JVWorker(A=A, α=α, β=β, a=a, b=b, grid_size=grid_size,
mc_size=mc_size, ɛ=ɛ, x_grid=x_grid, f_rvs=f_rvs)
@jax.jit
def g(jv, x, ϕ):
"""Transition function for human capital accumulation."""
return jv.A * (x * ϕ)**jv.α
@jax.jit
def π(s):
"""Search effort function."""
return jnp.sqrt(s)
Now we define the Bellman operator T, i.e.
where
When we represent \(v\), it will be with a JAX array v giving values on grid x_grid.
But to evaluate the right-hand side of (47.3), we need a function, so
we use JAX interpolation of v on x_grid.
@jax.jit
def state_action_values(jv, s_phi, x, v):
"""
Computes the value of state-action pair (x, s, phi) given value function v.
"""
s, ϕ = s_phi
β = jv.β
x_grid, f_rvs = jv.x_grid, jv.f_rvs
v_func = lambda x_val: jnp.interp(x_val, x_grid, v)
# Monte Carlo integration over offers
def compute_offer_value(u):
return v_func(jnp.maximum(g(jv, x, ϕ), u))
integral = jnp.mean(jax.vmap(compute_offer_value)(f_rvs))
q = π(s) * integral + (1 - π(s)) * v_func(g(jv, x, ϕ))
return x * (1 - ϕ - s) + β * q
@jax.jit
def T(jv, v):
"""
The Bellman operator.
"""
x_grid, ɛ = jv.x_grid, jv.ɛ
def maximize_at_x(x):
# Create grid for optimization
search_grid = jnp.linspace(ɛ, 1, 15)
def objective(s_phi):
s, ϕ = s_phi
# Return negative value if constraint violated
constraint_satisfied = s + ϕ <= 1.0
value = state_action_values(jv, s_phi, x, v)
return jnp.where(constraint_satisfied, value, -jnp.inf)
# Grid search over feasible (s, ϕ) pairs
s_vals, phi_vals = jnp.meshgrid(search_grid, search_grid)
s_phi_pairs = jnp.stack(
[s_vals.ravel(), phi_vals.ravel()], axis=1)
# Evaluate objective at all grid points
values = jax.vmap(objective)(s_phi_pairs)
max_idx = jnp.argmax(values)
return values[max_idx]
return jax.vmap(maximize_at_x)(x_grid)
@jax.jit
def get_greedy(jv, v):
"""
Computes the v-greedy policy.
"""
x_grid, ɛ = jv.x_grid, jv.ɛ
def greedy_at_x(x):
# Create grid for optimization
search_grid = jnp.linspace(ɛ, 1, 15)
def objective(s_phi):
s, ϕ = s_phi
# Return negative value if constraint violated
constraint_satisfied = s + ϕ <= 1.0
value = state_action_values(jv, s_phi, x, v)
return jnp.where(constraint_satisfied, value, -jnp.inf)
# Grid search over feasible (s, ϕ) pairs
s_vals, phi_vals = jnp.meshgrid(search_grid, search_grid)
s_phi_pairs = jnp.stack(
[s_vals.ravel(), phi_vals.ravel()], axis=1)
# Evaluate objective at all grid points
values = jax.vmap(objective)(s_phi_pairs)
max_idx = jnp.argmax(values)
return s_phi_pairs[max_idx]
policies = jax.vmap(greedy_at_x)(x_grid)
return policies[:, 0], policies[:, 1] # s_policy, ϕ_policy
To solve the model, we will write a function that uses the Bellman operator and iterates to find a fixed point.
@jax.jit
def solve_model(jv, tol=1e-4, max_iter=1000):
"""
Solves the model by value function iteration
* jv is an instance of JVWorker
"""
def cond_fun(state):
v, i, error = state
return jnp.logical_and(error > tol, i < max_iter)
def body_fun(state):
v, i, error = state
v_new = T(jv, v)
error_new = jnp.max(jnp.abs(v - v_new))
return v_new, i + 1, error_new
# Initial state
v_init = jv.x_grid * 0.5 # Initial condition
init_state = (v_init, 0, tol + 1)
# Run iteration
v_final, iterations, final_error = jax.lax.while_loop(
cond_fun, body_fun, init_state)
return v_final
47.4. Solving for policies#
Let’s generate the optimal policies and see what they look like.
jv = create_jv_worker()
v_star = solve_model(jv)
s_star, ϕ_star = get_greedy(jv, v_star)
Here are the plots:
plots = [s_star, ϕ_star, v_star]
titles = ["s policy", "ϕ policy", "value function"]
fig, axes = plt.subplots(3, 1, figsize=(12, 12))
for ax, plot, title in zip(axes, plots, titles):
ax.plot(jv.x_grid, plot)
ax.set(title=title)
axes[-1].set_xlabel("x")
plt.show()
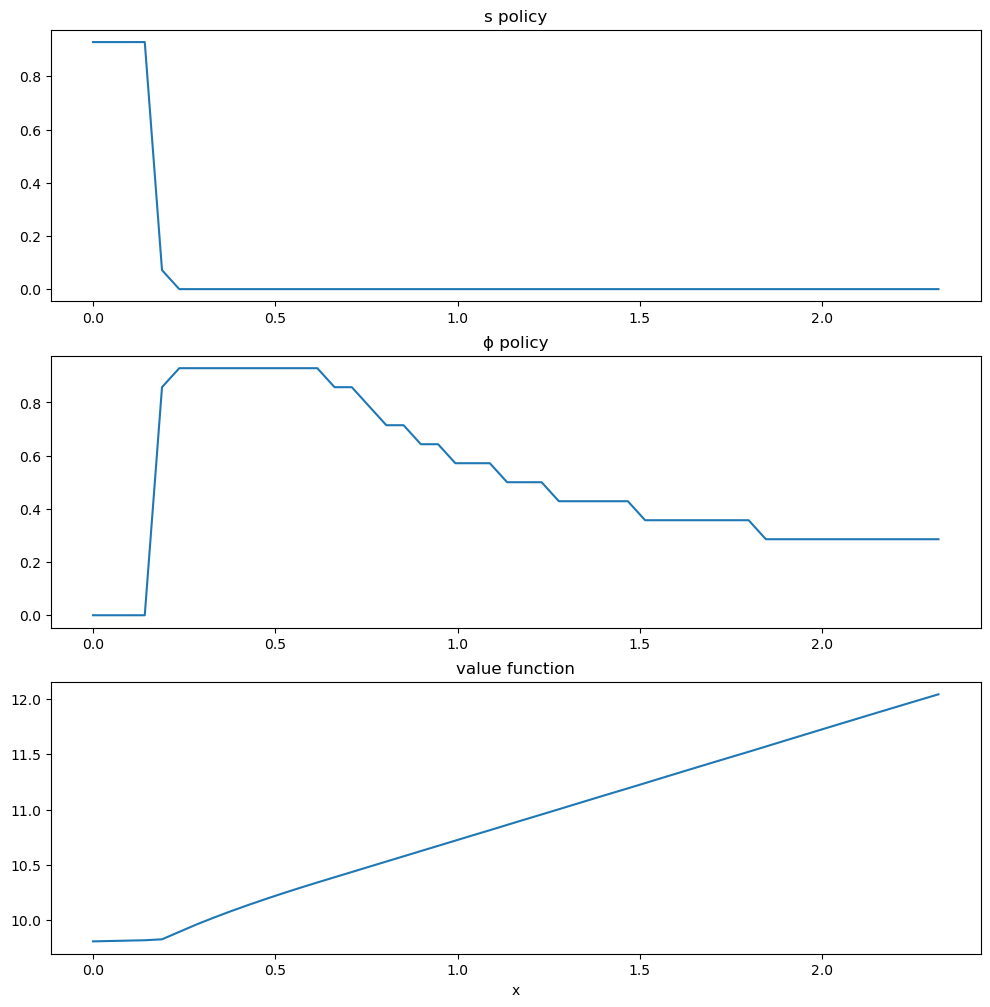
The horizontal axis is the state \(x\), while the vertical axis gives \(s(x)\) and \(\phi(x)\).
Overall, the policies match well with our predictions from above
Worker switches from one investment strategy to the other depending on relative return.
For low values of \(x\), the best option is to search for a new job.
Once \(x\) is larger, worker does better by investing in human capital specific to the current position.
47.5. Exercises#
Exercise 47.1
Let’s look at the dynamics for the state process \(\{x_t\}\) associated with these policies.
The dynamics are given by (47.1) when \(\phi_t\) and \(s_t\) are chosen according to the optimal policies, and \(\mathbb{P}\{b_{t+1} = 1\} = \pi(s_t)\).
Since the dynamics are random, analysis is a bit subtle.
One way to do it is to plot, for each \(x\) in a relatively fine grid
called plot_grid, a
large number \(K\) of realizations of \(x_{t+1}\) given \(x_t =
x\).
Plot this with one dot for each realization, in the form of a 45 degree diagram, setting
jv = JVWorker(grid_size=25, mc_size=50)
plot_grid_max, plot_grid_size = 1.2, 100
plot_grid = jnp.linspace(0, plot_grid_max, plot_grid_size)
fig, ax = plt.subplots()
ax.set_xlim(0, plot_grid_max)
ax.set_ylim(0, plot_grid_max)
By examining the plot, argue that under the optimal policies, the state \(x_t\) will converge to a constant value \(\bar x\) close to unity.
Argue that at the steady state, \(s_t \approx 0\) and \(\phi_t \approx 0.6\).
Solution to Exercise 47.1
Here’s code to produce the 45 degree diagram
jv = create_jv_worker(grid_size=25, mc_size=50)
f_rvs, x_grid = jv.f_rvs, jv.x_grid
v_star = solve_model(jv)
s_policy, ϕ_policy = get_greedy(jv, v_star)
# Turn the policy function arrays into actual functions
s = lambda y: jnp.interp(y, x_grid, s_policy)
ϕ = lambda y: jnp.interp(y, x_grid, ϕ_policy)
def h(x, b, u):
return (1 - b) * g(jv, x, ϕ(x)) + b * max(g(jv, x, ϕ(x)), u)
plot_grid_max, plot_grid_size = 1.2, 100
plot_grid = jnp.linspace(0, plot_grid_max, plot_grid_size)
fig, ax = plt.subplots(figsize=(8, 8))
ticks = (0.25, 0.5, 0.75, 1.0)
ax.set(xticks=ticks, yticks=ticks,
xlim=(0, plot_grid_max),
ylim=(0, plot_grid_max),
xlabel='$x_t$', ylabel='$x_{t+1}$')
ax.plot(plot_grid, plot_grid, 'k--', alpha=0.6) # 45 degree line
# Generate random values for plotting
key = jr.PRNGKey(0)
for x in plot_grid:
for i in range(jv.mc_size):
key, subkey = jr.split(key)
b = 1 if jr.uniform(subkey) < π(s(x)) else 0
u = f_rvs[i]
y = h(x, b, u)
ax.plot(x, y, 'go', alpha=0.25)
plt.show()
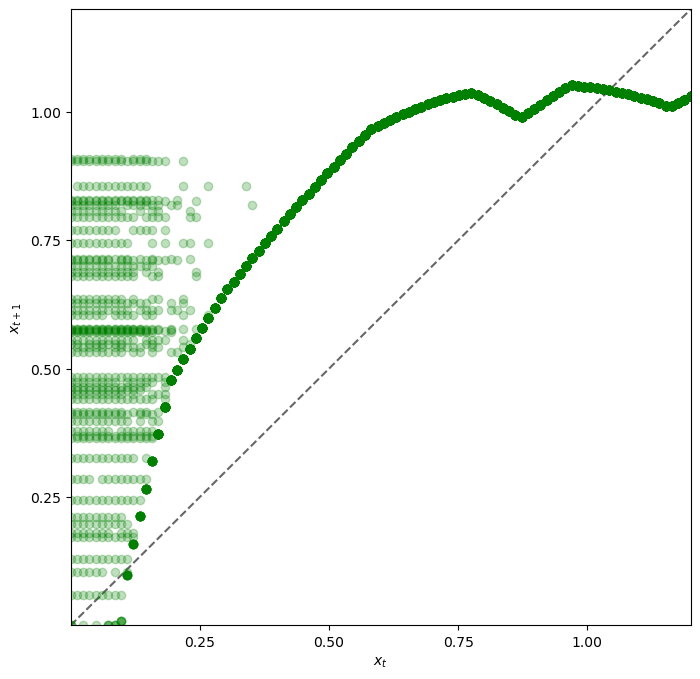
Looking at the dynamics, we can see that
If \(x_t\) is below about 0.2 the dynamics are random, but \(x_{t+1} > x_t\) is very likely.
As \(x_t\) increases the dynamics become deterministic, and \(x_t\) converges to a steady state value close to 1.
Referring back to the figure here we see that \(x_t \approx 1\) means that \(s_t = s(x_t) \approx 0\) and \(\phi_t = \phi(x_t) \approx 0.6\).
Exercise 47.2
In Exercise 47.1, we found that \(s_t\) converges to zero and \(\phi_t\) converges to about 0.6.
Since these results were calculated at a value of \(\beta\) close to one, let’s compare them to the best choice for an infinitely patient worker.
Intuitively, an infinitely patient worker would like to maximize steady state wages, which are a function of steady state capital.
You can take it as given—it’s certainly true—that the infinitely patient worker does not search in the long run (i.e., \(s_t = 0\) for large \(t\)).
Thus, given \(\phi\), steady state capital is the positive fixed point \(x^*(\phi)\) of the map \(x \mapsto g(x, \phi)\).
Steady state wages can be written as \(w^*(\phi) = x^*(\phi) (1 - \phi)\).
Graph \(w^*(\phi)\) with respect to \(\phi\), and examine the best choice of \(\phi\).
Can you give a rough interpretation for the value that you see?
Solution to Exercise 47.2
The figure can be produced as follows
jv = create_jv_worker()
def xbar(ϕ):
A, α = jv.A, jv.α
return (A * ϕ**α)**(1 / (1 - α))
ϕ_grid = jnp.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(9, 7))
ax.set(xlabel=r'$\phi$')
ax.plot(ϕ_grid, [xbar(ϕ) * (1 - ϕ) for ϕ in ϕ_grid], label=r'$w^*(\phi)$')
ax.legend()
plt.show()
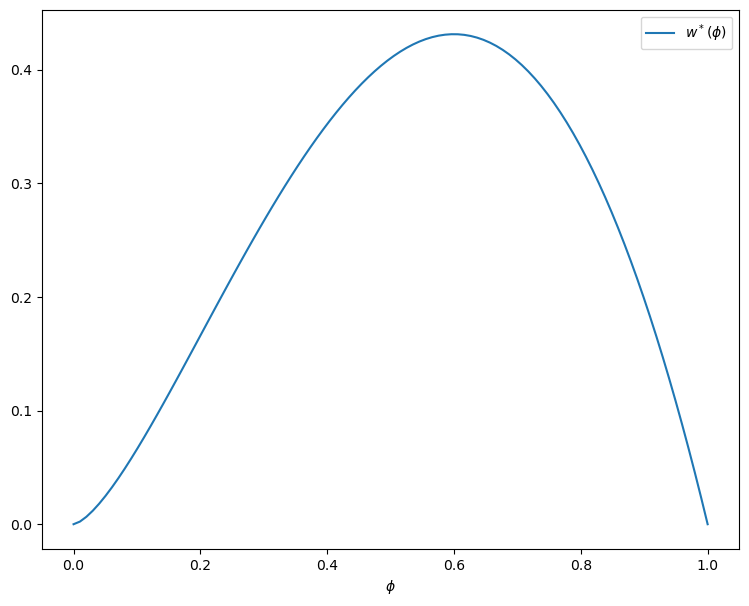
Observe that the maximizer is around 0.6.
This is similar to the long-run value for \(\phi\) obtained in Exercise 47.1.
Hence the behavior of the infinitely patent worker is similar to that of the worker with \(\beta = 0.96\).
This seems reasonable and helps us confirm that our dynamic programming solutions are probably correct.